True random numbers can’t hurt you … they’re not real. (Or are they?)
It looks like somebody is trying to hide your presents? Can you go trace them back and figure out their secrets?
Connect using nc ctf.csd.lol 5040.
Category
Points
Author
Reverse engineering
120
kolmus
| 1 | 12/18 7:14 pm | |
| 2 | 12/18 7:31 pm | |
| 3 | 12/18 8:37 pm | |
| 4 | 12/19 1:09 am | |
| 5 | 12/19 2:03 am | |
| 6 | 12/19 2:35 am | |
| 7 | 12/19 3:53 am | |
| 8 | 12/19 4:51 am | |
| 9 | 12/19 5:21 am | |
| 10 | 12/19 1:29 pm | |
| 11 | 12/19 3:34 pm | |
| 12 | 12/19 5:27 pm | |
| 13 | 12/19 10:01 pm | |
| 14 | 12/20 10:18 am | |
| 15 | 12/20 11:13 am | |
| 16 | 12/20 4:13 pm | |
| 17 | 12/21 2:02 pm | |
| 18 | 12/22 3:09 am | |
| 19 | 12/22 6:07 am | |
| 20 | 12/22 3:21 pm | |
| 21 | 12/22 4:14 pm | |
| 22 | 12/23 3:41 pm | |
| 23 | 12/23 4:00 pm | |
| 24 | 12/23 5:43 pm | |
| 25 | 12/25 9:51 am | |
| 26 | 12/25 3:04 pm | |
| 27 | 12/26 12:46 pm | |
| 28 | 12/26 1:24 pm | |
| 29 | 12/27 12:39 am | |
| 30 | 12/27 4:01 am | |
| 31 | 12/27 9:54 am |
True random numbers can’t hurt you … they’re not real. (Or are they?)
It looks like somebody is trying to hide your presents? Can you go trace them back and figure out their secrets?
Connect using nc ctf.csd.lol 5040.
There are no penalties for viewing hints. Hints are released 12 hours and 24 hours after the challenge releases.
raul_26 (Fl4gged)'s write-up was selected as the best write-up submitted for this challenge.
View this write-up on GitHubFirst, I opened the binary in binary ninja and saw the main function:
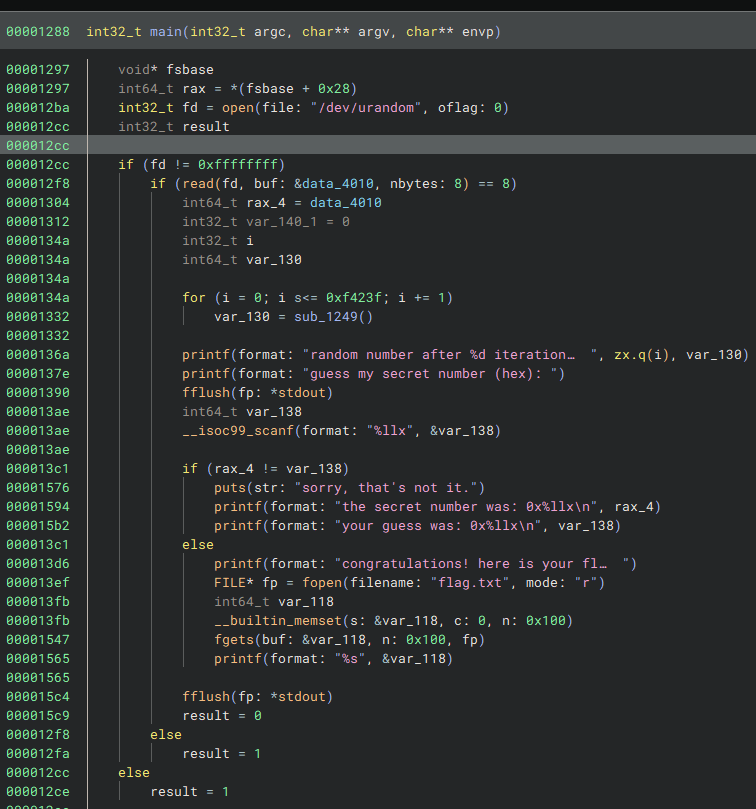
And this additional function:
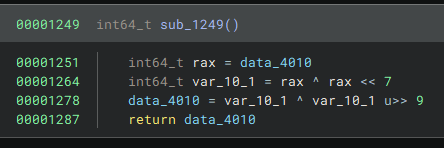
Basically, this program encodes a random number by iterating 1,000,000 times over it and applying the sub_1249() function. To get the flag, it is needed to "guess" the random number before this encoding process. To reverse the encoding, I used this article, which explains how to break xor shift. Let's take the example from the article:
y = x ^ (x >> 3)
y is known, and x needs to be found. Let's say y and x are both 8 bits and represent each bit as a letter:
y = ijklmnop x = abcdefgh
From y = x ^ (x >> 3) it can be said that:
(eq1) abcdefgh ^ 000abcde -------- ijklmnop
It can be seen that ijk=abc since a^0=a, so just by looking at y the first 3 bits of x are known. In the article, there are more details on how they found the following formula:
x = y ^ (y >> 3) ^ (y >> 6)
But basically it states that (remember the x and y notations):
(eq2) abclmnop ^ 000abclm ^ 000000ab -------- abcdefgh
Alright, the first 3 bits make sense, what about the rest, why is this true? Well, looking at (eq1) l=a^d and we want to get d, which is the initial bit of x (we are looking for x remember?) so by doing l^a we get d. For m n the similar logic is applied. Finally, for the last two bits it is known that o=g^d and l=a^d, thus from (eq2) we have g^d^a^d^a which is exactly g (similar logic is for the last bit). In the article, there is also a more general formula:
x = y; for (i = 1; i * shift < bitSize; i++) x ^= y >> (i * shift);
This is the most important part. In this case the bitSize is 64 so to reverse the encoding I did:
import numpy as np
def reverse_sub_1249(data_4010):
a = data_4010 ^ (data_4010 >> 9) ^ (data_4010 >> 18) ^ (data_4010 >> 27) ^ (data_4010 >> 36) ^ (data_4010 >> 45) ^ (data_4010 >> 54) ^ (data_4010 >> 63)
z = a ^ (a << 7) ^ (a << 14) ^ (a << 21) ^ (a << 28) ^ (a << 35) ^ (a << 42) ^ (a << 49) ^ (a << 56) ^ (a << 63)
return z
data_4010 = np.uint64(0xe415efccd9f117c4)
for i in range(0,1000000):
data_4010 = reverse_sub_1249(data_4010)
print(f"Recovered x: {data_4010:#016x}")
Basically, I just applied the general formula and did the calculations in the opposite order. The numpy function just bounds the variable data_4010 to not exceed 64 bits. Then I just connected to the server, used the encoded hex values printed as input for my program, and got the secret number.
Flag: csd{M47H_15nT_7H4t_5cARY_N0w_15_I7?}